InTempo Ares e l’importanza della linea dei numeri nel potenziamento delle difficoltà aritmetiche

- Argomenti: Altri BES
Le difficoltà aritmetiche
Molti alunni di tutti i gradi scolastici hanno un rapporto difficile con la matematica: alcuni la percepiscono difficile, alcuni inutile, altri astratta. Potremmo dire che lo stesso si applica al mondo adulto: capita di frequente, infatti, di sentire persone anche con alti livelli culturali ammettere in tutta innocenza, a volte pure con un pizzico di orgoglio, la propria assoluta mancanza di competenza e comprensione della matematica.
La parola chiave per questo breve articolo sarà proprio astratta. Perché avvicina la percezione di alcuni bambini con alcune delle difficoltà che, secondo molti modelli alla base della discalculia evolutiva, essi effettivamente incontrano: dire “9” è qualcosa di astratto, se a 9 il bambino non associa mentalmente una quantità. In particolare, una quantità che può confrontare con 11 e 13, e ordinare in una sequenza di altri numeri.
La stessa astrattezza si può osservare più avanti nel corso degli studi, finché la matematica non viene finalmente applicata. Molti di noi ricordano probabilmente la difficoltà nella comprensione del concetto di derivata … finché la fisica non ci ha insegnato che, applicata a spazio e tempo, questa è la formalizzazione matematica del concetto di velocità istantanea: la semantica della matematica prende allora forma e diventa meno astratta.
Torniamo alle difficoltà aritmetiche: due concetti molto importanti sono quello dei processi di cognizione numerica e del sistema del calcolo.
- I processi di cognizione numerica ci permettono la comprensione del numero nelle sue diverse rappresentazioni, ed in particolare:
- i processi semantici risolvono il più basilare dei problemi dell’astrattezza: associano ad un numero espresso nella forma più semplice, la cifra (ad esempio 4) una quantità (4 uova, 4 carte, 4 punti …)
- i processi lessicali sono alla base della conversione da numeri rappresentati come cifre a numeri come lettere (e viceversa)
- i processi sintattici permettono di costruire e manipolare i numeri: dando un significato alla posizione delle 10 cifre dallo 0 al 9 si costruiscono numeri complessi
Il sistema del calcolo permette il passo successivo: compiere operazioni sui numeri.
Un punto fondamentale sono i processi semantici, come possiamo aiutare bambini che faticano a dare un significato ai numeri? La linea dei numeri (Gersten e altri, 2009) è un ottimo strumento, proprio permettendo il passaggio dall’astratto al concreto grazie alla rappresentazione su una linea della quantità che un numero rappresenta. Di più, collocare sulla linea diversi numeri dà anche concretezza visiva ai confronti fra i numeri. Gli alunni imparano che ogni numero ha una specifica posizione sulla linea dei numeri e i numeri successivi sono sequenziati secondo uno schema specifico. Inoltre, imparando che ogni intervallo di uguale dimensione su una linea numerica rappresenta un’unità specifica, possono estendere le proprie capacità dal “contare un numero di oggetti in un insieme” al “contare unità di lunghezza” (Van de Walle, Karp e Bay-Williams, 2012).
Imparare questi concetti aiuta a sviluppare una rappresentazione mentale dell’ordine e della grandezza dei numeri che possono essere utilizzati per manipolare i numeri. Quindi per fare calcoli.
Il processo inverso è altrettanto importante: dalla posizione sulle linea al numero. Questo aiuta i bambini nel processo di rappresentazione simbolica, ovvero la traduzione dal visuale all’astratto, che spesso risulta deficitaria in caso di discalculia (Gersten et al., 2009; Witzel, Mercer, & Miller, 2003).
InTempo Ares
Posizionamento di un numero sulla linea, determinazione del numero che una posizione sulla linea rappresenta e calcoli sulla linea sono proprio i tre esercizi fondamentali che troviamo in Ares, la App progettata da Anastasis e Patrizio Tressoldi per il potenziamento dei processi semantici e del sistema del calcolo di InTempo, il servizio per l’individuazione precoce ed il potenziamento delle difficoltà negli apprendimenti di Anastasis e Sos Dislessia (intempo.net). In Ares la linea dei numeri è considerata un ambiente di lavoro visuale in cui svolgere attività a difficoltà progressiva, sia sulla dimensione delle linee sia sull’impatto del sistema di aiuti. La progressione della difficoltà è gestita in maniera autoadattiva: se il bambino risponde bene, si alza un po’ l’asticella della difficoltà, altrimenti gli esercizi vengono riproposti nella stessa modalità. Per aiutare i bambini con associate difficoltà di lettura, Ares propone tutti gli esercizi anche con consegna vocale.
Si comincia quindi con le prime due tipologie di esercizi (dal numero alla posizione sulla linea, e dalla posizione al numero) sulla linea del 10: in prima battuta fornendo il massimo degli aiuti quando il bambino sbaglia; mano a mano che le risposte diventano corrette, gli stessi esercizi vengono riproposti con aiuti meno importanti a fronte degli errori, fino alla scomparsa totale. Prima di passare alla linea successiva, il bambino deve svolgere gli esercizi senza aiuto.
In particolare, i livelli del sistema di aiuti sono 3:
- tutti gli aiuti disponibili con diminuzione progressiva: massimo supporto all’inizio (tutte le tacche con tutte le etichette) con attenuazione graduale degli aiuti se il bambino risponde correttamente, fino alla scomparsa di tutti gli aiuti.
- solo tacche sugli errori: a fronte di un errore, compare una tacca sulla posizione toccata
- nessun aiuto
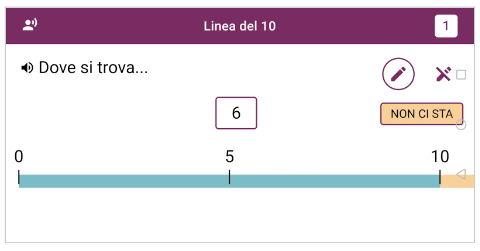
È sempre possibile utilizzare lo strumento penna segna tacche: toccando la penna in alto a destra (si veda figura 1) si disegnano tacche al fine di visualizzare un numero di riferimento (ad esempio un 5 per collocare un 6 su una linea del 10 senza aiuti). Anche la penna favorisce i processi semantici permettendo ragionamenti basati sul confronto fra quantità.
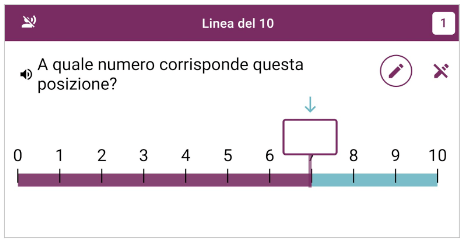
Si procede con la linea del 20, e successivamente vengono introdotti gli esercizi del terzo tipo: addizioni, sottrazioni, moltiplicazioni e divisioni.
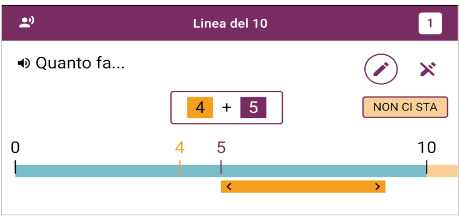
La figura precedente introduce anche un nuovo strumento: il regolo (mobile o fisso). In questo caso, è presente un regolo mobile (barra arancione) che rappresenta la quantità dell’operando in arancione (il 4) ed è già posizionato correttamente: il bambino toccherà quindi la linea alla fine del regolo mobile. Nei compiti successivi il regolo non sarà più posizionato correttamente, ed il bambino potrà spostarlo. Il regolo sarà poi fisso, ed alla fine non sarà più visibile, sempre nella logica di diminuzione progressiva propria della difficoltà 1. Gli esercizi di Ares sono tarati in base alla classe frequentata dagli alunni su 3 parametri:
- il numero di compiti per ogni esercizio;
- la durata della sessione;
- il livello di arrivo (in termini di dimensione della linea e tipologia di esercizio).
La seguente tabella illustra questi parametri in base alla classe frequentata:
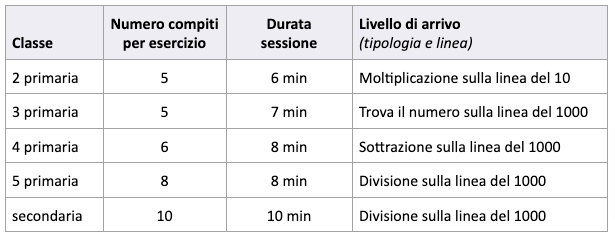
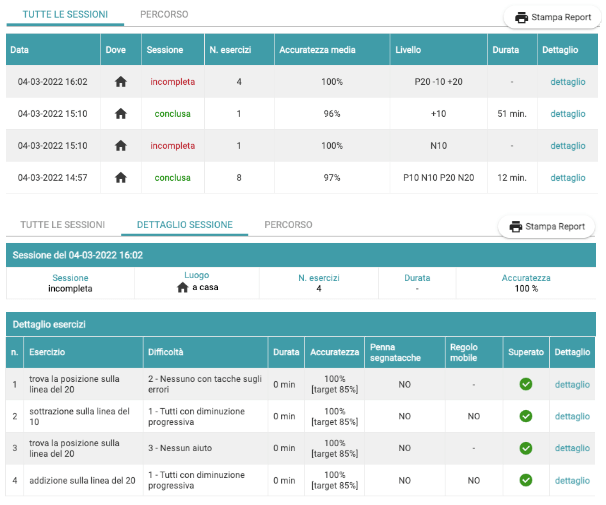
Ares è pensata per un lavoro di 6-10 minuti 3 volte la settimana per un periodo che può variare dalle due settimane ai due mesi in base al livello di difficoltà dei bambini. Il lavoro viene svolto sia insieme all’insegnante (o alla psicologa/logopedista), sia a casa in autonomia: un sistema di monitoraggio – accessibile solo dal portale InTempo – permette di effettuare una supervisione del lavoro svolto sia con gli operatori stessi sia a casa.
Infine, la linea dei numeri è anche efficace come strumento compensativo per bambini con difficoltà aritmetiche: come esempio virtuoso si riporta che nel 2008, su suggerimento di Giacomo Stella – partner e ideatore delle prove di identificazione precoce e di alcune App di potenziamento di InTempo – la scuola primaria Marmorta di Molinella (BO) ha dotato tutti i banchi di sistemi adesivi con la lin ea dei numeri (e la tavola pitagorica).
A cura di Andrea Frascari – Referente progetto InTempo e Giovanna Cialdini – Laboratori Anastasis